Kalman Filtering for STC/PCR smoothing
Introduction
Kalman Filters have been developed in the 1960s for state estimation of not directly-measurable noisy signals in linear or quasi-linear systems. They have been used with great success in the past for Avionics and Image Processing systems.
For a good introduction to State Estimation Techniques and some links to similiar or even more advanced approaches please check out the papers in the Link section.
Some trivial Sample Code
Below you see some simple example code showing how trivial an implementation of a 1-D Kalman filter becomes.
/* compile with gcc -g -Wall -O0 -o kalman kalman.c -lm */
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int main (int argc, char **argv)
{
int i = 0;
float x_next, x;
float P_next, P;
float K, Q, R, z;
P = 1; /* Estimation Error Covariance */
Q = 1.0 / 100000.0; /* needs to get adjusted to actual noise parameters */
R = 0.1 * 0.1; /* needs to get adjusted to actual noise parameters */
x = 0.0; /* Initial State Estimate */
printf ("# t\tx\tz\n");
while (i < 20000) {
z = ((float) random() / RAND_MAX) + sin (i/1000.0);
x_next = x;
P_next = P + Q;
K = P_next / (P_next + R);
x = x_next + K * (z - x_next);
P = (1 - K) * P_next;
printf ("%d\t", i);
printf ("%f\t", x);
printf ("%f\n", z);
i++;
}
return 0;
}
This codelet produces the following output (rendered with gnuplot, red: noisy input signal, green: filtered output). Please note that this picture contains 20000 correction points (PCR inputs in the DVB sense) -- that's quite a long correction interval. Start gnuplot on your own and zoom in to see the smooth local adjustments.
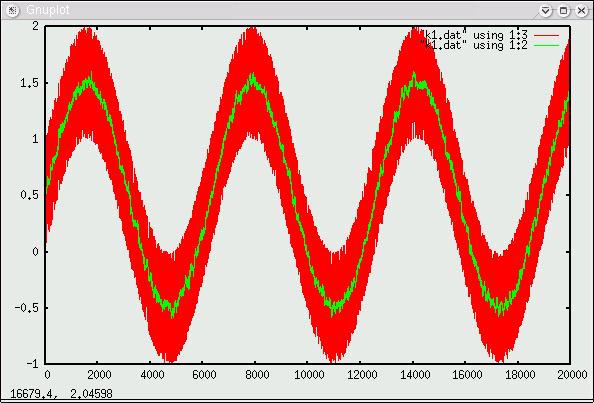
In order to estimate the clock of the broadcasting server from noisy PCR values you design a trivial linear model (e.g. z = PCR/hostclock difference, x = host/server clock offset). More sophisticated higher-order models are also imagineable.
Kalman filters perform well if you have a rough idea of the process and measurement noise parameters in advance (like it is the case in DVB STC estimation applications: you know upper bounds of the PCI/FIFO burst latencies quite exactly). If these parameters are badly chooses a Kalman filter can become instable. Hinfinity Filters overcome this limitation and are unconditionally stable, but less accurate than a optimally tuned kalman filter. There have been proposals to combine both filters by linear blending, please check the Innovatia.com website for details.